ПРИНЦИПЫ РАСЧЕТА АНАЛИЗИРУЮЩЕЙ СИСТЕМЫ
Пусть значения цветовых координат, взятых нами первичных цветов R, G, В по международной системе будут:
х'r, у'r, z'r; x'g, y'g, z'g; x'b, y'b, z'b
Если спектральное распределение для света, отраженного объектом, есть Е (л), а цвет его F, то по свойствам кривых сложения цвет F может быть составлен из наших трех первичных R, G, В согласно цветовому уравнению:
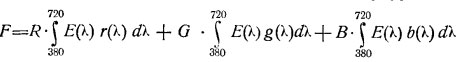
где r(л), g(л), b(л) — кривые сложения для первичных R, G, В.
Пусть спектральная чувствительность пластинок будет Sr(л); Sg(л); Sb(л). Тогда действие света с распределением энергии E(л) на пластинку выразится в виде:
Пусть спектральная чувствительность пластинок будет Sr(л); Sg(л); Sb(л). Тогда действие света с распределением энергии E(л) на пластинку выразится в виде:
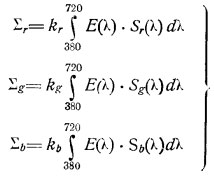
где kr, kg, kb — коэфициенты, зависящие от экспозиции.
Непрозрачности негативов и прозрачности диапозитивов будут (при гамма=1) пропорциональны этим величинам.
При репродуцировании прозрачности диапозитивов определят количества складываемых первичных, а потому цвет F, полученный на репродукции, будет:
Непрозрачности негативов и прозрачности диапозитивов будут (при гамма=1) пропорциональны этим величинам.
При репродуцировании прозрачности диапозитивов определят количества складываемых первичных, а потому цвет F, полученный на репродукции, будет:
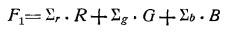
Сравнивая равенства (1), (2) и (3) мы видим, что для точного совпадения цветов на репродукции с цветами оригинала (F=F1) необходимо и достаточно, чтобы
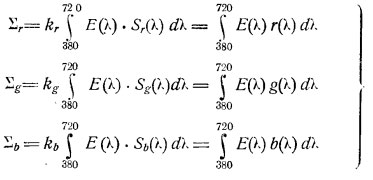
Так как равенства (4) должны иметь место для любого Е(л) (для любых излучений оригинала), то необходимым и достаточным условием точной передачи любых цветов оригинала является:
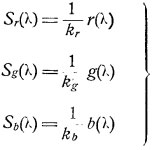
Иначе говоря, ординаты кривых спектральной чувствительности пластинок должны быть пропорциональны ординатам кривых сложения взятых первичных R, G, В.
Кривые сложения для первичных R, G, В не трудно вычислить из стандартных кривых сложения для системы X, Y, Z.
Так как кооординаты кривых сложения являются координатами цветов спектра, то к ним применима общая формула (см. гл. I, § 18), связывающая цветовые координаты одного и того же цвета относительно различных первичных, т. е.
Кривые сложения для первичных R, G, В не трудно вычислить из стандартных кривых сложения для системы X, Y, Z.
Так как кооординаты кривых сложения являются координатами цветов спектра, то к ним применима общая формула (см. гл. I, § 18), связывающая цветовые координаты одного и того же цвета относительно различных первичных, т. е.
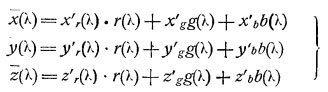
Решая эту систему уравнений относительно r(л), g(л) b(л) получим:
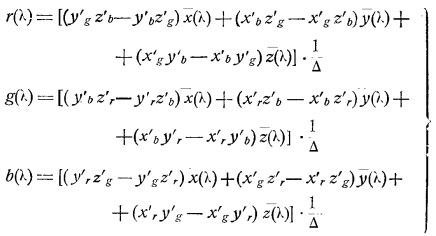
где дельта постоянный множитель, равный
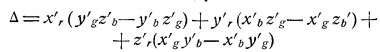
Так как искомые кривые спектральной чувствительности Sr(л), Sg(л), Sb(л) должны быть пропорциональны кривым сложения, мы можем отбросить постоянный множитель 1\дельта. По этой же причине можно заменить, если угодно, цветовые координаты x'r, y'r, z'r и т. д. пропорциональными им трехцветными коэфициентами. Таким образом мы получаем формулу, позволяющую с помощью стандартных кривых сложения МОК х(л), у(л), z(л) и цветовых координат (трехцветных коэфициентов) взятых нами первичных R, G, B найти кривые относительной спектральной чувствительности пластинок Sr(л), Sg(л), Sb(л), обеспечивающих идеальную цветопередачу.
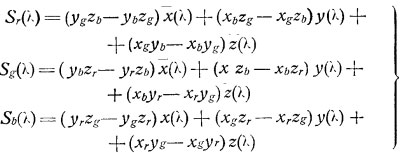
Фактически вычисление производится так: сначала вычисляют величины, стоящие в скобках. Затем, .взяв таблицу стандартных кривых сложения, помножают цифры первой колонки таблицы [х(л)] на первую скобку, вторую колонку [у(л)] на вторую и третью колонку [z(л)] на третью скобку первого уравнения. Беря для каждого (л) сумму трех полученных таким путем произведений, мы найдем Sr(л). Таким же образом вычисляются и две другие функции.
Вычисленные таким образом спектральные чувствительности для случая монохроматических синтезирующих первичных 700, 535 и 400 приведены на рис. 38.
Мы уже разбирали ранее результаты аддитивного синтеза с помощью этих первичных и нашли, что с помощью только положительных количеств их невозможно получить точную передачу всех цветов, включая и спектральные с полной насыщенностью.
Вследствие этого вычисленные кривые спектральной чувствительности, приведенные на рис. 38, в некоторых местах принимают отрицательные значения, соответствующие отрицательным количествам первичных, необходимым для воспроизведения соответствующего спектрального.
Вычисленные таким образом спектральные чувствительности для случая монохроматических синтезирующих первичных 700, 535 и 400 приведены на рис. 38.
Мы уже разбирали ранее результаты аддитивного синтеза с помощью этих первичных и нашли, что с помощью только положительных количеств их невозможно получить точную передачу всех цветов, включая и спектральные с полной насыщенностью.
Вследствие этого вычисленные кривые спектральной чувствительности, приведенные на рис. 38, в некоторых местах принимают отрицательные значения, соответствующие отрицательным количествам первичных, необходимым для воспроизведения соответствующего спектрального.
Передача насыщенности еще более ухудшается в том случае, когда мы применяем ненасыщенные первичные, представляющие собой довольно широкие полосы спектра. Производя, например, расчет для S(л) в случае первичных, изображенных на рис. 32, мы получим кривые спектральной чувствительности (рис. 39), отрицательные части в которых, в особенности для Sr, гораздо более развиты. Разумеется, невозможно придать фотографической пластинке спектральную чувствительность, меньшую нуля для некоторых л, илидобиться этого с помощью каких бы то ни было светофильтров, так как последние способны самое большее свести чувствительность до нуля.
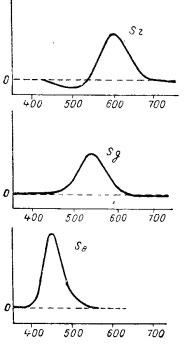
Рис. 38. Спектральная чувствительность анализирующей системы для монохроматических первичных рис. 30
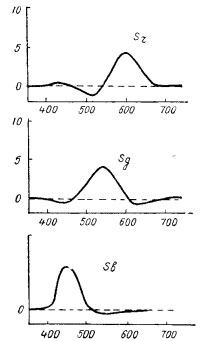
Рис. 39. Спектральная чувствительность анализирующей системы для первичных рис. 32
Невозможность воспроизведения отрицательных частей кривых спектральной чувствительности вызывает, конечно, некоторую ошибку в передаче цвета. Естественно, что эта ошибка будет тем большей, чем больше по размеру отрицательная часть, которой пренебрегают. Величина и значение этой ошибки будет выяснена позже.
