Система колориметрических характеристик, изложенная в главе I, позволяя построить стройную номенклатуру цветов, не дает, однако, возможности выразить степень различия между различными цветами, воспринимаемыми визуально. Между тем вопрос о восприятии различий между цветами имеет существеннейшее значение и для интересу­ющей нас проблемы цветной репродукции. В этом случае мы должны в первую очередь установить порог различи­мости для основных колориметрических величин, т.е. уста­новить те минимальные изменения цветового тона, насы­щенности и светлоты, которые еще можно заметить гла­зом. Очевидно, что при задаче воспроизведения цвета, ко­торая будет обсуждена в главе III, мы вправе требовать, чтобы цветовые характеристики нашей репродукции отли­чались от соответствующих величин оригинала не более чем на упомянутые порожные значения.
Проблема установления закономерностей, управляющих различением цветовых оттенков, принадлежит к числу труд­нейших и наименее разработанных отделов колориметрии, составляя часть так называемой высшей метрики цвета.
Наилучше изученным является вопрос о восприятии различий в яркости (светлоте) в зависимости от силы света. Эта зависимость может быть сформулирована математи­чески в виде так называемого закона Вебера-Фехнера.
Суть этого закона сводится к тому, что глаз оценивает как различие по яркости не абсолютные, а относительные изменения интенсивности света. Математически это можно записать так:

 

 

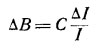
где дельта B — различие в яркости, соответствующее увеличе­нию интенсивности I на величину дельта I; С—коэфициент пропорциональности.
Следовательно одинаковые различия в яркости вызы­ваются одинаковыми относительными изменениями интен­сивности. Если эти изменения настолько малы, что их можно считать бесконечно малыми, то мы можем, записав уравнение в диференциальной форме, проинтегриро­вать его:

 

 

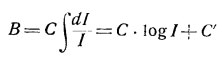
что и дает математическую формулировку закона Вебера-Фехнера.
Ощущение яркости возрастает пропорционально лога­рифму интенсивности света. Отсюда следует, что яркости возрастают в арифметической прогрессии, когда соответ­ствующие интенсивности света увеличиваются в геомет­рической.
При сравнении двух объектов различной освещенности величина различия в их яркостях будет, очевидно, пропор­циональна логарифму отношения освещенностей, т. е.

 

 

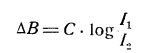
Если это отношение ниже известного предела, то глаз уже не воспринимает различия в яркости этих объектов. Эта предельная величина носит обычно название предела различаемое. В нарушение закона Вебера-Фехнера при больших колебаниях яркости света наблюдается некоторая (порой даже значительная) зависимость предела различае-мости от яркости. Наименьшей величины он достигает для больших, хорошо и равномерно освещенных поверх­ностей (например, легкие облака). Малейшее разнообразие в сравниваемых поверхностях влечет за собой значитель­ное возрастание порога различаемости и для объектов со множеством деталей (например, листва, кирпичная стена и т. п.) достигает даже при наиболее благоприятных ус­ловиях освещения до 25 — 30%.
Для черно-белого фотографического отпечатка средняя величина порога различаемости составляет по Гольдбергу около 15%, колеблясь от 5% для ярких светов до 25% для теней. Таким образом при визуальном сравнении двух отпечатков различной силы мы улавливаем их различие, если оно оказывается не меньшим, чем 15 — 20%. Такая точность оценки оказывается далеко не достаточной для цветной фотографии.