ВЫРАЖЕНИЕ ЦВЕТОВОГО ТОНА И НАСЫЩЕННОСТИ С ПОМОЩЬЮ ТРЕХЦВЕТНЫХ КОЭФИЦИЕНТОВ
Рассмотрение диаграммы цветности дает нам возможность интерпретировать любой реальный цвет еще и другим способом. В самом деле все реальные цвета, лежащие внутри кривой спектральных цветов, но вне пунктирных линий на рис. 23, могут рассматриваться как смесь „белого" осветителя с некоторым спектральным, лежащим на продолжении линии, соединяющей белую точку с цветовой точкой данного стимула. Так например, зеленый стимул, определяющийся точкой G, можно рассматривать как смесь белого С с чистым спектральным с длиной волны 506(рис. 23).
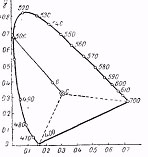
Рис. 23. Нахождение цветового тона и насыщенности
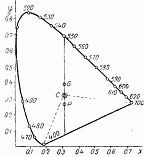
Рис. 24 Нахождение цветового тона для пурпурных цветов
Рассматривая цвета с такой точки зрения, легко видеть, что окраска цвета, т. е. его цветовой тон, будет характеризоваться длиной волны того спектрального, который в смеси с белым в точности воспроизводит исследуемый цвет. Эта длина волны называется доминирующей длиной волны и в дальнейшем будет сокращенно обозначаться как ДДВ. Она, таким образом, служит количественной характеристикой цветного тона.
При таком способе характеристики цветового тона встречаются затруднения в определении ДДВ для пурпурных тонов, которым, как известно, не соответствует никакой спектральный. В таком случае прибегают к искусственному приему: соединив данную цветовую точку Р с белой точкой С, продолжают эту линию за белую точку до пересечения с линией спектральных (рис. 24). Длина
волны этого спектрального, например 550, принимается условно за ДДВ данного пурпурного и для отличия либо ставится в скобках, либо снабжается знаком -минус.
Легко видеть, что эта ДДВ является не чем иным, как длиной волны спектрального дополнительного к данному пурпурному.
В свете развитых нами представлений насыщенность цвета будет, очевидно, определяться долей чистого спектрального, входящего в его состав. Численное выражение насыщенности — чистоту цвета — можно получить, пользуясь нанесенными на графике линиями равной чистоты.
Таким образом мы располагаем двумя количественными способами выражения цвета: системой цветовых координат, которая является однозначным определением цвета и характеристикой цвета через ДДВ, и чистоту, характеризующими только цветность. Система цветовых координат незаменима при всякого рода расчетах, связанных со смешением цветов, вопросами передачи цвета и т. п. С Другой стороны, выражение цвета через ДДВ и чистоту более доступно непосредственному представлению, так как ассоциирует цвет с хорошо известными спектральными цветами.
Из трех качеств цвета, о которых речь шла выше, нам осталось еще количественно выразить только светлоту. При пользовании системой основных стимулов МОК это чрезвычайно упрощается, ибо при построении кривых смешения (рис. 19) функция у была выбрана таким образом, что она полностью совпадает со стандартной кривой видности. Так как ординаты кривой видности пропорциональны светлоте соответствующего цвета, то значения координаты у, пропорциональные значениям соответствующей ординаты кривой видности, дают непосредственно значение светлоты по отношению к светлоте идеально белого тела, которая принимается за 100%.
Если два окрашенных предмета дают при измерении одинаковые координаты, то их цвет при том же осветителе, каким они были освещены при измерении, должен быть одинаковым.
При других условиях освещения цвета этих предметов могут быть различными. Так например, два желтых предмета, один из которых отражает только желтые спектральные лучи, а другой — соответствующим образом подобранную смесь зеленых и красных лучей, могут быть одинаковы по цвету при освещении белым светом и быть совершенно различными при освещении монохроматическим желтым светом, скажем, от натриевой лампы.
Сравниваемые нами предметы могут быть одинаковыми по цвету при любом типе освещения и для всех наблюдателей только при полном совпадении их кривых спектрального отражения (или пропускания).
Следует сказать несколько слов еще об одной системе цветовых характеристик, предложенной Решем и оказывающейся очень полезной в ряде специальных случаев. Реш исходит из того, что для каждого реального цвета (имея в виду цвета несветящихся предметов) можно подобрать такой оптимальный цвет, который бы при данном освещении совпадал с измеряемым образцом как по тону, так и по насыщенности. Так как оптимальные цвета являются идеальными и на практике недостижимыми, то для получения тождества по светлоте мы должны в той или иной степени ослабить интенсивность такого оптимального, сделав ординаты его спектральной кривой равными не 0 и 1, а 0 и а (где а<1). Как мы уже видели, оптимальный цвет полностью характеризуется шириной выреза Sp и длиной волны, соответствующей его середине. Добавив к этому еще величину а, получим триаду величин Sp, лм и а, характеризующую по Решу любой цвет.
Возможен простой переход от системы цветовых координат к системе Реша и обратно, для чего служат специальные таблицы, приведенные в уже упоминаемом труде проф. Федорова.
Следует иметь в виду, что координаты Реша характеризуют положение данного цвета но отношению других цветов, возможных в условиях определенного освещения, а потому связь между координатами Реша и трехцветными для различных освещений будет различной. Таблицы, приведенные в книге проф. Федорова, рассчитаны на среднее дневное освещение.
При таком способе характеристики цветового тона встречаются затруднения в определении ДДВ для пурпурных тонов, которым, как известно, не соответствует никакой спектральный. В таком случае прибегают к искусственному приему: соединив данную цветовую точку Р с белой точкой С, продолжают эту линию за белую точку до пересечения с линией спектральных (рис. 24). Длина
волны этого спектрального, например 550, принимается условно за ДДВ данного пурпурного и для отличия либо ставится в скобках, либо снабжается знаком -минус.
Легко видеть, что эта ДДВ является не чем иным, как длиной волны спектрального дополнительного к данному пурпурному.
В свете развитых нами представлений насыщенность цвета будет, очевидно, определяться долей чистого спектрального, входящего в его состав. Численное выражение насыщенности — чистоту цвета — можно получить, пользуясь нанесенными на графике линиями равной чистоты.
Таким образом мы располагаем двумя количественными способами выражения цвета: системой цветовых координат, которая является однозначным определением цвета и характеристикой цвета через ДДВ, и чистоту, характеризующими только цветность. Система цветовых координат незаменима при всякого рода расчетах, связанных со смешением цветов, вопросами передачи цвета и т. п. С Другой стороны, выражение цвета через ДДВ и чистоту более доступно непосредственному представлению, так как ассоциирует цвет с хорошо известными спектральными цветами.
Из трех качеств цвета, о которых речь шла выше, нам осталось еще количественно выразить только светлоту. При пользовании системой основных стимулов МОК это чрезвычайно упрощается, ибо при построении кривых смешения (рис. 19) функция у была выбрана таким образом, что она полностью совпадает со стандартной кривой видности. Так как ординаты кривой видности пропорциональны светлоте соответствующего цвета, то значения координаты у, пропорциональные значениям соответствующей ординаты кривой видности, дают непосредственно значение светлоты по отношению к светлоте идеально белого тела, которая принимается за 100%.
Если два окрашенных предмета дают при измерении одинаковые координаты, то их цвет при том же осветителе, каким они были освещены при измерении, должен быть одинаковым.
При других условиях освещения цвета этих предметов могут быть различными. Так например, два желтых предмета, один из которых отражает только желтые спектральные лучи, а другой — соответствующим образом подобранную смесь зеленых и красных лучей, могут быть одинаковы по цвету при освещении белым светом и быть совершенно различными при освещении монохроматическим желтым светом, скажем, от натриевой лампы.
Сравниваемые нами предметы могут быть одинаковыми по цвету при любом типе освещения и для всех наблюдателей только при полном совпадении их кривых спектрального отражения (или пропускания).
Следует сказать несколько слов еще об одной системе цветовых характеристик, предложенной Решем и оказывающейся очень полезной в ряде специальных случаев. Реш исходит из того, что для каждого реального цвета (имея в виду цвета несветящихся предметов) можно подобрать такой оптимальный цвет, который бы при данном освещении совпадал с измеряемым образцом как по тону, так и по насыщенности. Так как оптимальные цвета являются идеальными и на практике недостижимыми, то для получения тождества по светлоте мы должны в той или иной степени ослабить интенсивность такого оптимального, сделав ординаты его спектральной кривой равными не 0 и 1, а 0 и а (где а<1). Как мы уже видели, оптимальный цвет полностью характеризуется шириной выреза Sp и длиной волны, соответствующей его середине. Добавив к этому еще величину а, получим триаду величин Sp, лм и а, характеризующую по Решу любой цвет.
Возможен простой переход от системы цветовых координат к системе Реша и обратно, для чего служат специальные таблицы, приведенные в уже упоминаемом труде проф. Федорова.
Следует иметь в виду, что координаты Реша характеризуют положение данного цвета но отношению других цветов, возможных в условиях определенного освещения, а потому связь между координатами Реша и трехцветными для различных освещений будет различной. Таблицы, приведенные в книге проф. Федорова, рассчитаны на среднее дневное освещение.
