ДИАГРАММА ЦВЕТНОСТИ
Графическое представление цветов требовало бы трехмерной координатной системы, что не всегда удобно. Цветность может быть выражена путем нанесения коэфициентов х и у на обычную двумерную систему декартовых координат. Такой график называется диаграммой цветности (рис. 21). Сплошной линией на рисунке показано расположение чистых спектральных цветов, нанесенное на основании кривых смешения МОК.
Система прямоугольных координат является в настоящее время наиболее употребительной для выражения результатов цветных измерений. Раньше для этого чаще применяли равносторонний треугольник (так называемый цветовой треугольник или треугольник Максвелла), вершины которого соответствуют содержанию лишь одного первичного в количестве, равном единице. Трехцветные коэфи-циенты каждого цвета, соответствующего определенной точке внутри треугольника, определяются длиной перпендикуляров, опущенных от данной точки на три стороны треугольника. Из свойств равностороннего треугольника следует, что сумма перпендикуляров для всех точек внутри треугольника постоянна, что и требуется для трехцветных коэфициентов. Такой треугольник представлен на рис. 22.
Трехцветные коэфициенты определяют некоторую точку ("цветовая точка") на диаграмме цветности. Так, для нормальных осветителей значения цветовых координат, определяющих их цветовые точки („белая точка"), следующие:
осветитель А....х = 0,448; y= 0,407
Система прямоугольных координат является в настоящее время наиболее употребительной для выражения результатов цветных измерений. Раньше для этого чаще применяли равносторонний треугольник (так называемый цветовой треугольник или треугольник Максвелла), вершины которого соответствуют содержанию лишь одного первичного в количестве, равном единице. Трехцветные коэфи-циенты каждого цвета, соответствующего определенной точке внутри треугольника, определяются длиной перпендикуляров, опущенных от данной точки на три стороны треугольника. Из свойств равностороннего треугольника следует, что сумма перпендикуляров для всех точек внутри треугольника постоянна, что и требуется для трехцветных коэфициентов. Такой треугольник представлен на рис. 22.
Трехцветные коэфициенты определяют некоторую точку ("цветовая точка") на диаграмме цветности. Так, для нормальных осветителей значения цветовых координат, определяющих их цветовые точки („белая точка"), следующие:
осветитель А....х = 0,448; y= 0,407
осветитель В....х = 0,3485; у = 0,352
осветитель С....х = 0,310; у = 0,316
Диаграмма цветности обладает одним свойством, которое делает ее незаменимой для представления результатов оптического смешения двух или более стимулов. На рис. 21 некоторый красный представлен точкой R, некоторый зеленый — точкой G. Независимо от пропорций, в которых смешиваются эти два стимула, результирующий цвет будет всегда лежать на прямой, соединяющей R с G. Точное положение каждой точки, изображающей ту или иную смесь, может быть легко рассчитано по правилам, которые будут изложены в главе III.
Диаграмма цветности обладает одним свойством, которое делает ее незаменимой для представления результатов оптического смешения двух или более стимулов. На рис. 21 некоторый красный представлен точкой R, некоторый зеленый — точкой G. Независимо от пропорций, в которых смешиваются эти два стимула, результирующий цвет будет всегда лежать на прямой, соединяющей R с G. Точное положение каждой точки, изображающей ту или иную смесь, может быть легко рассчитано по правилам, которые будут изложены в главе III.
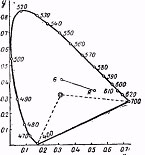
Рис. 21. Диаграмма цветности
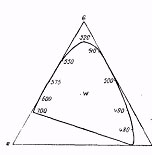
Рис. 22. Цветовой треугольник Максвелла
В силу такого свойства диаграммы цветности все реальные цвета должны лежать внутри плоскости, ограниченной кривой спектральных цветов.
Легко видеть, что на концах прямой, проведенной через „белую точку", будут лежать взаимно дополнительные цвета, причем количества их, необходимые для составления белого цвета, будут прэпорциональны длинам отрезков от белой до соответствующей цветной точки.
Легко видеть, что на концах прямой, проведенной через „белую точку", будут лежать взаимно дополнительные цвета, причем количества их, необходимые для составления белого цвета, будут прэпорциональны длинам отрезков от белой до соответствующей цветной точки.